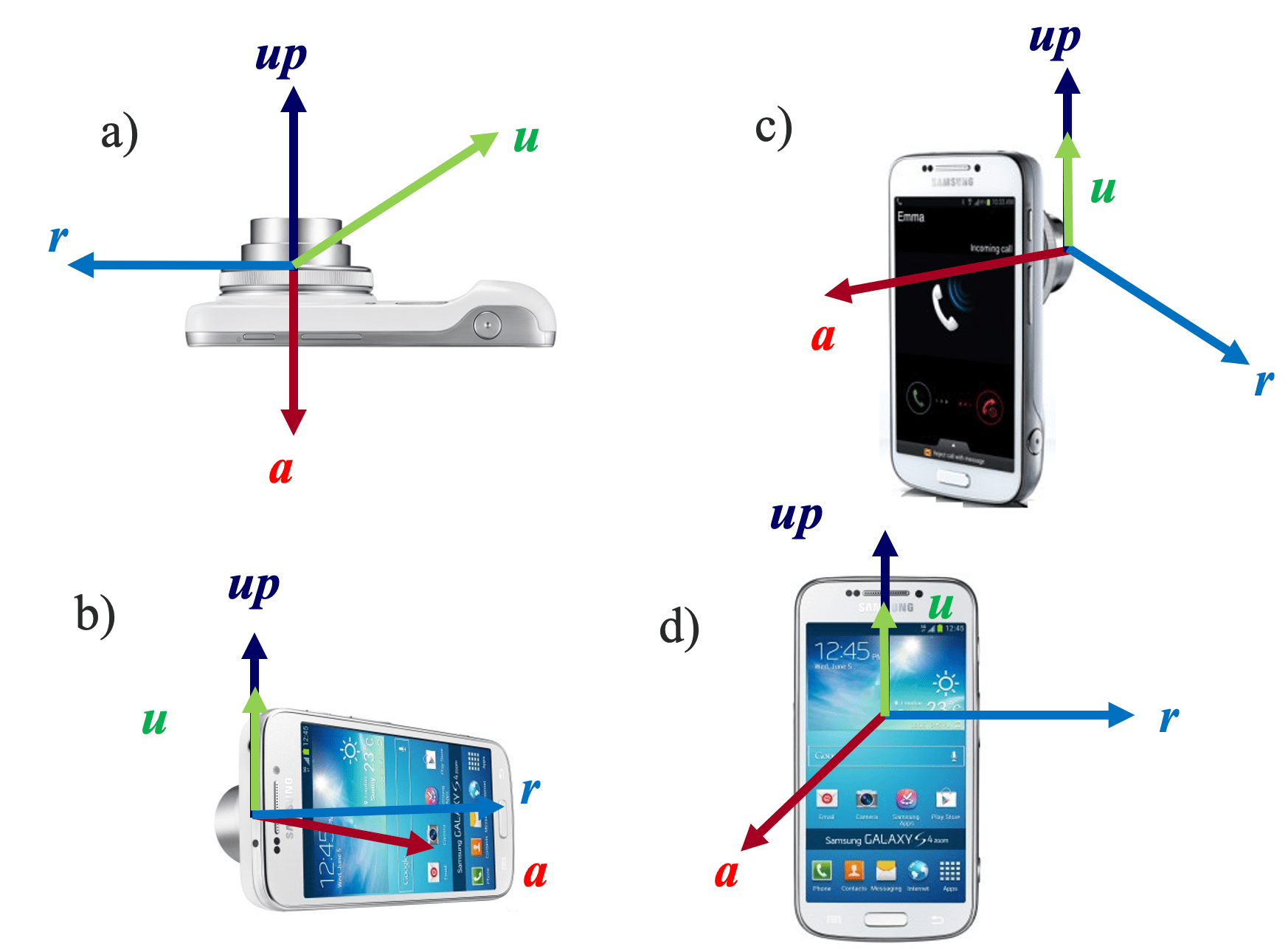
CG-Assignment-1
Question-1
Consider the unit sphere centered at the origin as shown in the figure below. An implicit equation of the sphere is
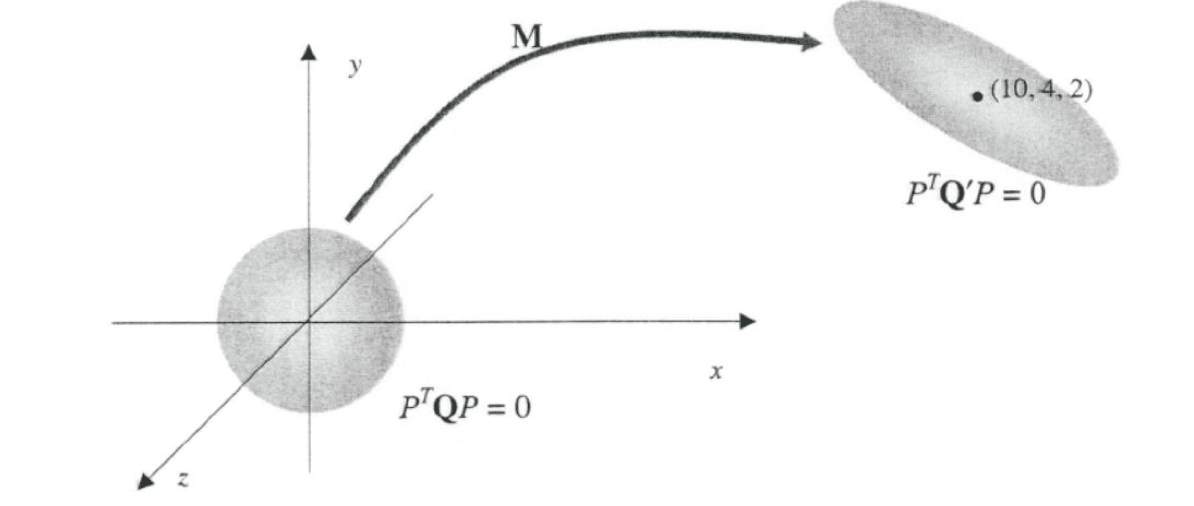
Give the matrix S that scales the sphere to the ellipsoid whose radii along the x-, y-, and z-axes are 3, 0.5, and 0.3, respectively. What is the inverse of S?
Given the matrix R that rotates the ellipsoid -45 degrees about the z-axis. What is the inverse of R?
Give the matrix T that translates the rotated ellipsoid to (10, 4, 2). What is the inverse of T?
Let M be the matrix representing the overall transformations described in (b), (c), and (d). Give a formula for M in terms of S, R, and T.
Give a formula for
Let the equation of the ellipsoid by
Brief Solution:
The original sphere has the quadratic form:
After applying the transformation matrix
To derive
This expands to:
Thus, the new quadratic form matrix is:
Question-2
The following shows a perspective projection where the eye is at the origin, the viewing direction is the opposite of the z-axis, and the projection plane is
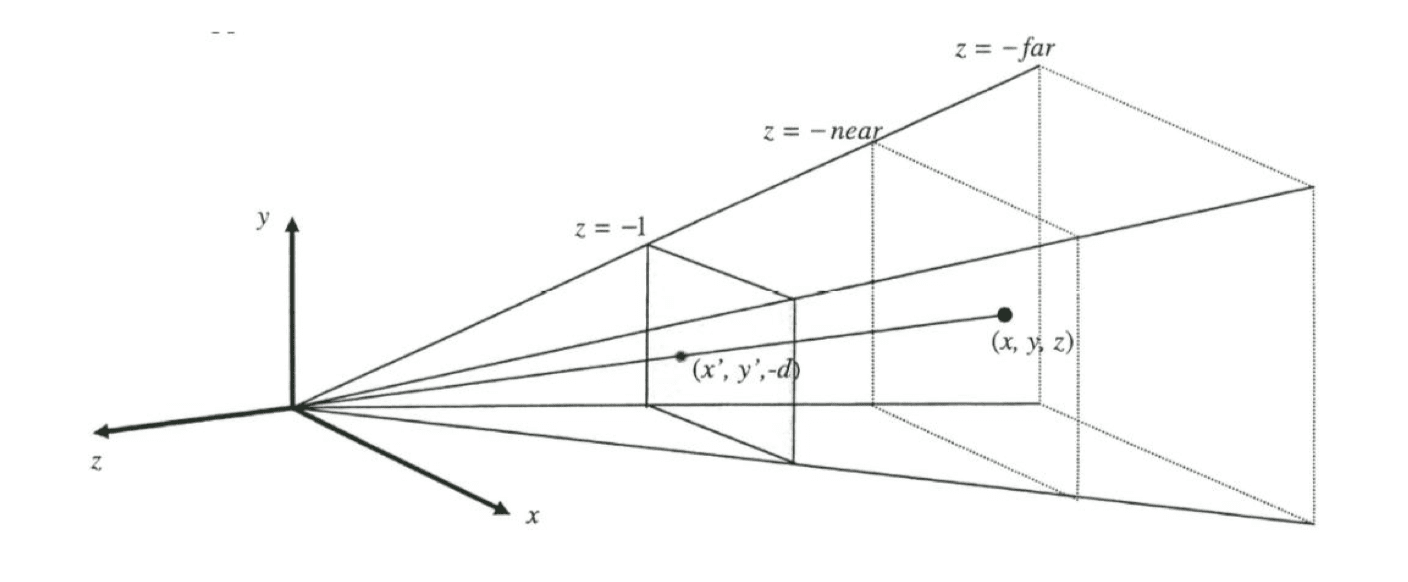
A point at
Give the
Since
Question-3
1. Write down the steps and the composite matrix for rotating 30 degrees about point
2. Write down the composite matrix for rotating 30 degrees about z-axis, then rotating 60 degrees about y-axis.
3. Write down the rotation matrix for rotating 30 degrees about the axis
According to Rodrigues' Rotation Formula
where:
is the identity matrix, , is the skew-symmetric matrix of the unit vector .
Compute the Skew-Symmetric Matrix
The unit vector along
The skew-symmetric matrix
Compute
Compute the Rotation Matrix
Using
After computation, the rotation matrix is:
4. Given eye point
Question-4
Please draw